ABM2
Propagates the state vector forward one time step using the Adams-Bashforth-Moulton 2nd-order method.
Back to IVP Solver Toolbox Contents.
Contents
Syntax
F = ABM2(f,t,F,h)
Description
F = ABM2(f,t,y,h) updates the 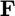 matrix, F, for the next sample time, given the
matrix, F, for the next sample time, given the 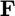 matrix at the current time t, the function f(t,y) defining the ODE
matrix at the current time t, the function f(t,y) defining the ODE 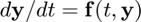 , and the step size h.
, and the step size h.
Input/Output Parameters
| Variable | Symbol | Description | Format | |
| Input | f | multivariate, vector-valued function ( - inputs to f are the current time (t, 1×1 double) and the current state vector (y, p×1 double) - output of f is the state vector derivative (dydt, p×1 double) at the current time/state |
1×1 function_handle |
|
| t | current sample time | 1×1 double |
||
| F | p×3 double |
|||
| h | step size | 1×1 double |
||
| Output | F | p×3 double |