tableau2eqns
Propagation equations from Butcher tableau.
Back to IVP Solver Toolbox Contents.
Contents
- Syntax
- Description
- Input/Output Parameters
- Note
- Example #1: RK2 (Midpoint method)
- Example #2: RK2 (Heun's method)
- Example #3: (Ralston's method)
- Example #4: (Kutta's third-order method)
- Example #5: (Heun's third-order method)
- Example #6: (Ralston's third-order method)
- Example #7: (Strong Stability Preserving Runge-Kutta third-order method)
- Example #8: (Runge-Kutta fourth-order method)
- Example #9: (Ralston's fourth-order method)
- Example #10: (3/8-Rule fourth-order method)
Syntax
tableau2eqns(T)
tableau2eqns(T,name)
tableau2eqns(__,'decimal')
Description
tableau2eqns(T) prints the propagation equations corresponding to a Butcher Tableau defined by T to the Command Window.
tableau2eqns(T,name) does the same as the syntax above, but labels the equations with the name specified by name.
tableau2eqns(...,'decimal') does the same as the syntaxes above, but writes the coefficients of the propagation equations in decimal form.
Input/Output Parameters
| Variable | Symbol | Description | Format | |
| Input | T | - | Butcher tableau | (s+1)×(s+1) double |
| name | - | (OPTIONAL) name of Runge-Kutta method corresponding to the Butcher tableau | 1×1 string |
|
| type | - | (OPTIONAL) print coefficients as 'decimal' or 'fraction' (defaults to 'fraction') | char |
Note
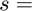number of stages of the explicit Runge-Kutta method
Example #1: RK2 (Midpoint method)
T = [0 0 0;
1/2 1/2 0;
0 0 1];
tableau2eqns(T,"RK2 (Midpoint method)");
RK2 (Midpoint method) --------------------- k1 = f(t(n), y(n)) k2 = f(t(n) + h/2, y(n) + h*k1/2) y(n+1) = y(n) + h(k2)
Example #2: RK2 (Heun's method)
T = [0 0 0;
1 1 0;
0 1/2 1/2];
tableau2eqns(T,"RK2 (Heun's method)");
RK2 (Heun's method) ------------------- k1 = f(t(n), y(n)) k2 = f(t(n) + h, y(n) + h*k1) y(n+1) = y(n) + (h/2)(k1 + k2)
Example #3: (Ralston's method)
T = [0 0 0;
2/3 2/3 0;
0 1/4 3/4];
tableau2eqns(T,"RK2 (Ralston's method)");
RK2 (Ralston's method) ---------------------- k1 = f(t(n), y(n)) k2 = f(t(n) + 2h/3, y(n) + 2h*k1/3) y(n+1) = y(n) + (h/4)(k1 + 3k2)
Example #4: (Kutta's third-order method)
T = [0 0 0 0;
1/2 1/2 0 0;
1 -1 2 0;
0 1/6 2/3 1/6];
tableau2eqns(T,"RK3 (Kutta's third-order method)");
RK3 (Kutta's third-order method) -------------------------------- k1 = f(t(n), y(n)) k2 = f(t(n) + h/2, y(n) + h*k1/2) k3 = f(t(n) + h, y(n) - h*k1 + 2h*k2) y(n+1) = y(n) + (h/6)(k1 + 4k2 + k3)
Example #5: (Heun's third-order method)
T = [0 0 0 0;
1/3 1/3 0 0;
2/3 0 2/3 0;
0 1/4 0 3/4];
tableau2eqns(T,"RK3 (Heun's third-order method)");
RK3 (Heun's third-order method) ------------------------------- k1 = f(t(n), y(n)) k2 = f(t(n) + h/3, y(n) + h*k1/3) k3 = f(t(n) + 2h/3, y(n) + 2h*k2/3) y(n+1) = y(n) + (h/4)(k1 + 3k3)
Example #6: (Ralston's third-order method)
T = [0 0 0 0;
1/2 1/2 0 0;
3/4 0 3/4 0;
0 2/9 1/3 4/9];
tableau2eqns(T,"RK3 (Ralston's third-order method)");
RK3 (Ralston's third-order method) ---------------------------------- k1 = f(t(n), y(n)) k2 = f(t(n) + h/2, y(n) + h*k1/2) k3 = f(t(n) + 3h/4, y(n) + 3h*k2/4) y(n+1) = y(n) + (h/9)(2k1 + 3k2 + 4k3)
Example #7: (Strong Stability Preserving Runge-Kutta third-order method)
T = [0 0 0 0;
1 1 0 0;
1/2 1/4 1/4 0;
0 1/6 1/6 2/3];
tableau2eqns(T,"SSPRK3 (Strong Stability Preserving Runge-Kutta third-order method)");
SSPRK3 (Strong Stability Preserving Runge-Kutta third-order method) ------------------------------------------------------------------- k1 = f(t(n), y(n)) k2 = f(t(n) + h, y(n) + h*k1) k3 = f(t(n) + h/2, y(n) + h*k1/4 + h*k2/4) y(n+1) = y(n) + (h/6)(k1 + k2 + 4k3)
Example #8: (Runge-Kutta fourth-order method)
T = [0 0 0 0 0;
1/2 1/2 0 0 0;
1/2 0 1/2 0 0;
1 0 0 1 0;
0 1/6 1/3 1/3 1/6];
tableau2eqns(T,"RK4 (Runge-Kutta fourth-order method)");
RK4 (Runge-Kutta fourth-order method) ------------------------------------- k1 = f(t(n), y(n)) k2 = f(t(n) + h/2, y(n) + h*k1/2) k3 = f(t(n) + h/2, y(n) + h*k2/2) k4 = f(t(n) + h, y(n) + h*k3) y(n+1) = y(n) + (h/6)(k1 + 2k2 + 2k3 + k4)
Example #9: (Ralston's fourth-order method)
T = [0 0 0 0 0;
0.4 0.4 0 0 0;
0.45573725 0.29697761 0.15875964 0 0;
1 0.21810040 -3.05096516 3.83286476 0;
0 0.17476028 -0.55148066 1.20553560 0.17118478];
tableau2eqns(T,"RK4 (Ralston's fourth-order method)",'decimal');
RK4 (Ralston's fourth-order method) ----------------------------------- k1 = f(t(n), y(n)) k2 = f(t(n) + 0.40000000h, y(n) + 0.40000000h*k1) k3 = f(t(n) + 0.45573725h, y(n) + 0.29697761h*k1 + 0.15875964h*k2) k4 = f(t(n) + h, y(n) + 0.21810040h*k1 - 3.05096516h*k2 + 3.83286476h*k3) y(n+1) = y(n) + h(0.17476028k1 - 0.55148066k2 + 1.20553560k3 + 0.17118478k4)
Example #10: (3/8-Rule fourth-order method)
T = [0 0 0 0 0;
1/3 1/3 0 0 0;
2/3 -1/3 1 0 0;
1 1 -1 1 0;
0 1/8 3/8 3/8 1/8];
tableau2eqns(T,"3/8-Rule fourth-order method");
3/8-Rule fourth-order method ---------------------------- k1 = f(t(n), y(n)) k2 = f(t(n) + h/3, y(n) + h*k1/3) k3 = f(t(n) + 2h/3, y(n) - h*k1/3 + h*k2) k4 = f(t(n) + h, y(n) + h*k1 - h*k2 + h*k3) y(n+1) = y(n) + (h/8)(k1 + 3k2 + 3k3 + k4)