`cdirectional`

Directional derivative of a multivariate, scalar-valued function using the central difference approximation.

Back to Numerical Differentiation Toolbox Contents.

Syntax
Description
Input/Output Parameters
Note
Example
See also

Syntax

Dv = cdirectional(f,x0,v)
Dv = cdirectional(f,x0,v,h)

Description

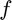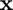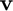Dv = cdirectional(f,x0,v) numerically evaluates the directional derivative of $f$ with respect to $\mathbf{x}$ at $\mathbf{x}=\mathbf{x}_{0}$ in the direction of $\mathbf{v}$ using the central difference approximation with a default relative step size of 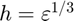$h=\varepsilon^{1/3}$ , where 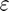$\varepsilon$ is the machine zero.

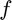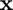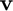Dv = cdirectional(f,x0,v,h) numerically evaluates the directional derivative of $f$ with respect to $\mathbf{x}$ at $\mathbf{x}=\mathbf{x}_{0}$ in the direction of $\mathbf{v}$ using the central difference approximation with a user-specified relative step size $h$ .

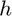Input/Output Parameters

Variable Symbol Description Format

Input f $f(\mathbf{x})$ multivariate, scalar-valued function ( $f:\mathbb{R}^{n}\rightarrow\mathbb{R}$ ) 1×1
function_handle

x0 $\mathbf{x}_{0}$ evaluation point n×1
double

v $\mathbf{v}$ vector defining direction of differentiation n×1
double

h $h$ (OPTIONAL) relative step size (defaults to $h=\varepsilon^{1/3}$) 1×1
double

Output Dv $\nabla_{\mathbf{v}}f(\mathbf{x}_{0})=\nabla f(\mathbf{x}_{0})^{T}\mathbf{v}$ directional derivative of $f$ with respect to $\mathbf{x}$ in the direction of $\mathbf{v}$ , evaluated at $\mathbf{x}=\mathbf{x}_{0}$ 1×1
double

Note

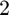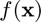This function requires evaluations of $f(\mathbf{x})$ .
This implementation does not assume that 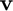$\mathbf{v}$ is a unit vector.

Example

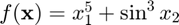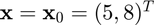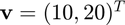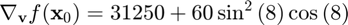Approximate the directional derivative of $f(\mathbf{x})=x_{1}^{5}+\sin^{3}{x_{2}}$ at $\mathbf{x}=\mathbf{x}_{0}=(5,8)^{T}$ in the direction of $\mathbf{v}=(10,20)^{T}$ using the cdirectional function, and compare the result to the true result of $\nabla_{\mathbf{v}}f(\mathbf{x}_{0})=31250+60\sin^{2}{(8)}\cos{(8)}$ .

Approximating the directional derivative,

f = @(x) x(1)^5+sin(x(2))^3;
x0 = [5;8];
v = [10;20];
Dv = cdirectional(f,x0,v)

Dv =

   3.1241e+04

Calculating the error,

error = Dv-(31250+60*sin(8)^2*cos(8))

error =

   9.1068e-06

	Variable	Symbol	Description	Format
Input	`f`	$f(\mathbf{x})$	multivariate, scalar-valued function ( $f:\mathbb{R}^{n}\rightarrow\mathbb{R}$ )	1×1 function_handle
	`x0`	$\mathbf{x}_{0}$	evaluation point	n×1 double
	`v`	$\mathbf{v}$	vector defining direction of differentiation	n×1 double
	`h`	$h$	(OPTIONAL) relative step size (defaults to $h=\varepsilon^{1/3}$)	1×1 double
Output	`Dv`	$\nabla_{\mathbf{v}}f(\mathbf{x}_{0})=\nabla f(\mathbf{x}_{0})^{T}\mathbf{v}$	directional derivative of $f$ with respect to $\mathbf{x}$ in the direction of $\mathbf{v}$ , evaluated at $\mathbf{x}=\mathbf{x}_{0}$	1×1 double

cdirectional