cpartial
Partial derivative of a multivariate, vector-valued function using the central difference approximation.
Back to Numerical Differentiation Toolbox Contents.
Contents
Syntax
pf = cpartial(f,x0,k) pf = cpartial(f,x0,k,h)
Description
pf = cpartial(f,x0,k) numerically evaluates the partial derivative of 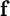 with respect to
with respect to 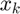 at
at  using the central difference approximation with a default relative step size of
using the central difference approximation with a default relative step size of 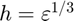 , where
, where 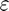 is the machine zero.
is the machine zero.
pf = cpartial(f,x0,k,h) numerically evaluates the partial derivative of 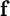 with respect to
with respect to 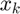 at
at  using the central difference approximation with a user-specified relative step size
using the central difference approximation with a user-specified relative step size 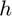 .
.
Input/Output Parameters
| Variable | Symbol | Description | Format | |
| Input | f | multivariate, vector-valued function ( |
1×1 function_handle |
|
| x0 | evaluation point | n×1 double |
||
| k | element of |
1×1 double |
||
| h | (OPTIONAL) relative step size (defaults to $h=\varepsilon^{1/3}$) | 1×1 double |
||
| Output | pf | partial derivative of |
m×1 double |
Note
- This function requires 2 evaluations of
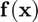 .
.
Example #1: Partial derivative of a scalar-valued function.
Approximate the partial derivative of  with respect to
with respect to 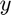 at at
at at 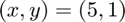 using the cpartial function, and compare the result to the true result of
using the cpartial function, and compare the result to the true result of
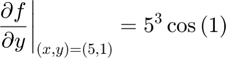
First, we rewrite this function as 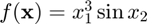 .
.
f = @(x) x(1)^3*sin(x(2));
Since the second component of 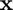 represents
represents 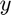 , to approximate the derivative, we use
, to approximate the derivative, we use
k = 2;
Approximating the partial derivative using the cpartial function,
pf = cpartial(f,[5;1],k)
pf = 67.5378
Calculating the error,
error = pf-5^3*cos(1)
error = -2.2063e-09
Example #2: Partial derivative of a vector-valued function.
Approximate the partial derivative of
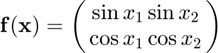
with respect to 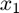 at
at 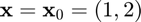 using the cpartial function, and compare the result to the true result of
using the cpartial function, and compare the result to the true result of
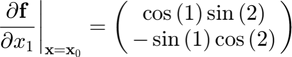
Defining the function in MATLAB,
f = @(x) [sin(x(1))*sin(x(2));cos(x(1))*cos(x(2))];
Approximating the partial derivative using the cpartial function,
x0 = [1;2]; % evaluation point k = 1; % element of x to differentiate with respect to pf = cpartial(f,x0,k) % differentiation
pf =
0.4913
0.3502
Calculating the error,
error = pf-[cos(1)*sin(2);-sin(1)*cos(2)]
error = 1.0e-11 * -0.9040 -0.8263