`iderivative`

Derivative of a univariate, vector-valued function using the complex-step approximation.

Back to Numerical Differentiation Toolbox Contents.

Syntax
Description
Input/Output Parameters
Note
Example #1: Derivative of a scalar-valued function.
Example #2: Derivative of a vector-valued function.
See also

Syntax

df = iderivative(f,x0)
df = iderivative(f,x0,h)

Description

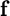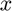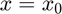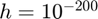df = iderivative(f,x0) numerically evaluates the derivative of $\mathbf{f}$ with respect to $x$ at $x=x_{0}$ using the complex-step approximation with a default step size of $h=10^{-200}$ .

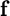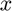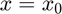df = iderivative(f,x0,h) numerically evaluates the derivative of $\mathbf{f}$ with respect to $x$ at $x=x_{0}$ using the complex-step approximation with a user-specified step size $h$ .

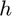Input/Output Parameters

Variable Symbol Description Format

Input f $\mathbf{f}(x)$ univariate, vector-valued function ( $\mathbf{f}:\mathbb{R}\rightarrow\mathbb{R}^{m}$ ) 1×1
function_handle

x0 $x_{0}$ evaluation point 1×1
double

h $h$ (OPTIONAL) step size (defaults to $h=10^{-200}$ ) 1×1
double

Output df $\dfrac{d\mathbf{f}}{dx}\bigg\rvert_{x=x_{0}}$ derivative of $\mathbf{f}$ with respect to $x$ , evaluated at $x=x_{0}$ m×1
double

Note

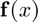This function requires 1 evaluation of $\mathbf{f}(x)$ .

Example #1: Derivative of a scalar-valued function.

Approximate the derivative of 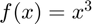$f(x)=x^{3}$ at 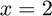using the iderivative function, and compare the result to the true result of .

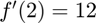Approximating the derivative,

f = @(x) x^3;
df = iderivative(f,2)

df =

    12

Calculating the error,

error = df-12

error =

     0

Example #2: Derivative of a vector-valued function.

Approximate the derivative of

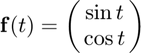
$\mathbf{f}(t)=\pmatrix{\sin{t}\cr\cos{t}}$

at 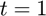using the iderivative function, and compare the result to the true result of

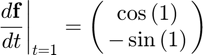
$\left.\frac{d\mathbf{f}}{dt}\right|_{t=1}=\pmatrix{\cos{(1)}\cr-\sin{(1)}}$