`RK3_ralston`

Propagates the state vector forward one time step using Ralston's third-order method (Runge-Kutta third-order method).

Syntax
Description
Input/Output Parameters
Note
Example
See also

Syntax

y_next = RK3_ralston(f,t,y,h)

Description

y_next = RK3_ralston(f,t,y,h) returns the state vector at the next sample time, y_next, given the current state vector y at time t, the function f(t,y) defining the ODE 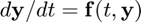$d\mathbf{y}/dt=\mathbf{f}(t,\mathbf{y})$ , and the step size h.

Input/Output Parameters

Variable Symbol Description Format

Input f $\mathbf{f}(t,\mathbf{y})$ multivariate, vector-valued function ( $\mathbf{f}:\mathbb{R}\times\mathbb{R}^{p}\rightarrow\mathbb{R}^{p}$ ) defining the ordinary differential equation $d\mathbf{y}/dt=\mathbf{f}(t,\mathbf{y})$
- inputs to f are the current time (t, 1×1 double) and the current state vector (y, p×1 double)
- output of f is the state vector derivative (dydt, p×1 double) at the current time/state 1×1
function_handle

t $t_{n}$ current sample time 1×1
double

y $\mathbf{y}_{n}=\mathbf{y}(t_{n})$ state vector (i.e. solution) at the current sample time p×1
double

h $h$ step size 1×1
double

Output y_next $\mathbf{y}_{n+1}=\mathbf{y}(t_{n+1})$ state vector (i.e. solution) at the next sample time, $t_{n+1}=t_{n}+h$ p×1
double

Note

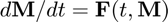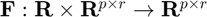This documentation is written specifically for the case of vector-valued ODEs. However, this function can also be used for matrix-valued ODEs of the form $d\mathbf{M}/dt=\mathbf{F}(t,\mathbf{M})$ , where $\mathbf{F}:\mathbf{R}\times\mathbf{R}^{p\times r}\rightarrow\mathbf{R}^{p\times r}$ .

Example

Consider the initial value problem

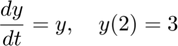
$\frac{dy}{dt}=y,\quad y(2)=3$

Find the solution 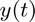until 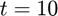using RK3_ralston. Then, compare your result to the solution found by solve_ivp using Ralston's 3rd-order method.

First, let's define our ODE (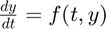 $\frac{dy}{dt}=f(t,y)$ ) and initial condition in MATLAB.

f = @(t,y) y;
y2 = 3;

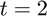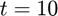Let's define a time vector between $t=2$ and $t=10$ with a spacing of $h=0.01$ .

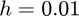h = 0.01;
t = (2:h:10)';

Solving for 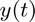$y(t)$ using RK3_ralston and comparing the result to the result obtained using solve_ivp with Ralston's 3rd-order method,

% preallocate vector to store solution
y = zeros(size(t));

% store initial condition
y(1) = y2;

% solving using "RK3_ralston"
for i = 1:(length(t)-1)
    y(i+1) = RK3_ralston(f,t(i),y(i),h);
end

% solving using "solve_ivp"
[t_ivp,y_ivp] = solve_ivp(f,[2,10],y2,h,'RK3 Ralston');

% maximum absolute error between the two results
max(abs(y_ivp-y))

ans =

     1.533408067189157e-09

As expected, the two methods obtain identical results.

	Variable	Symbol	Description	Format
Input	`f`	$\mathbf{f}(t,\mathbf{y})$	multivariate, vector-valued function ( $\mathbf{f}:\mathbb{R}\times\mathbb{R}^{p}\rightarrow\mathbb{R}^{p}$ ) defining the ordinary differential equation $d\mathbf{y}/dt=\mathbf{f}(t,\mathbf{y})$ - inputs to `f` are the current time (`t`, 1×1 double) and the current state vector (`y`, p×1 double) - output of `f` is the state vector derivative (`dydt`, p×1 double) at the current time/state	1×1 function_handle
	`t`	$t_{n}$	current sample time	1×1 double
	`y`	$\mathbf{y}_{n}=\mathbf{y}(t_{n})$	state vector (i.e. solution) at the current sample time	p×1 double
	`h`	$h$	step size	1×1 double
Output	`y_next`	$\mathbf{y}_{n+1}=\mathbf{y}(t_{n+1})$	state vector (i.e. solution) at the next sample time, $t_{n+1}=t_{n}+h$	p×1 double

RK3_ralston