ihessian
Hessian of a multivariate, scalar-valued function using the complex-step and central difference approximations.
Back to Numerical Differentiation Toolbox Contents.
Contents
Syntax
H = ihessian(f,x0) H = ihessian(f,x0,hi,hc)
Description
H = ihessian(f,x0) numerically evaluates the Hessian of 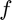 with respect to
with respect to 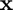 at
at  using a hybrid of complex-step and central difference approximations with default step sizes of
using a hybrid of complex-step and central difference approximations with default step sizes of 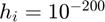 (an absolute step size) and
(an absolute step size) and 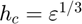 (a relative step size), respectively, where
(a relative step size), respectively, where 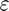 is the machine zero.
is the machine zero.
H = ihessian(f,x0,hi,hc) numerically evaluates the Hessian of 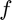 with respect to
with respect to 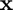 at
at  using a hybrid of complex-step and central difference approximations with user-specified step sizes
using a hybrid of complex-step and central difference approximations with user-specified step sizes 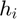 and
and 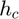 , respectively.
, respectively.
Input/Output Parameters
| Variable | Symbol | Description | Format | |
| Input | f | multivariate, scalar-valued function ( |
1×1 function_handle |
|
| x0 | evaluation point | n×1 double |
||
| hi | (OPTIONAL) step size for complex-step approximation (defaults to |
1×1 double |
||
| hc | (OPTIONAL) relative step size for central difference approximation (defaults to |
1×1 double |
||
| Output | H | Hessian of |
n×n double |
Note
- This function requires
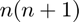 evaluations of
evaluations of 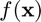 .
.
Example
Approximate the Hessian of 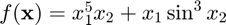 at
at 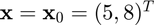 using the ihessian function, and compare the result to the true result of
using the ihessian function, and compare the result to the true result of
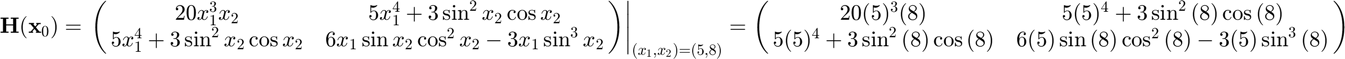
Approximating the Hessian,
f = @(x) x(1)^5*x(2)+x(1)*sin(x(2))^3; x0 = [5;8]; H = ihessian(f,x0)
H =
1.0e+04 *
2.0000 0.3125
0.3125 -0.0014
Calculating the error,
error = H-[20*5^3*8,5*5^4+3*sin(8)^2*cos(8);5*5^4+3*sin(8)^2*cos(8),...
6*5*sin(8)*cos(8)^2-3*5*sin(8)^3]
error =
1.0e-05 *
0.1036 0.0011
0.0011 0.0049